先日、この記事が話題になっていました⇒www.4gamer.net
これは、ゲーム情報紹介サイトの 4Gamer.net に掲載された記事で、内容は、ソーシャルゲームなどでよく見られるガチャに関連して、ある確率で当たるくじを何回も引いた場合にどのくらい当たるか、という事を解説したものです。
詳しくはリンク先を見ていただくとして、記事は、確率の基本的な知識の紹介である事や、100回引けば1度くらいはほぼ確実に当たるのではないかというような直観が必ずしも正しく無いのを周知させる、という所が教訓的であるし、また、ゲーム関連サイトがこの話題を採り上げるという点でも、とても意義のあるものだと思います。
さて、そんな良記事ですが、それでもやはり、確率の話というのは難しいもので、説明を見ても、なんかすっきりしないな、といったような感想を持たれた方も、おられるやも知れません。そこで、私は今回、この問題について、もう少し直感的直観的に把握出来そうなものを、作ってみました。
内容としては、なるべく視覚的な直感で解りやすいようにする事を心がけ、また、ゲームにまつわる話題でもあるので、少しゲームっぽくする事を試みました。以下がそれです。
上に、10×10のマス目があります。この一つ一つのマス目が、くじを1回引く事を表す、と考えて下さい。マス目は全部で100ありますので、この全体で、くじを100回引く事を表現します。
紹介した記事に合わせて、1回のくじで当たりの出る確率を、1%としましょう。それを100回繰り返す訳です。
ここで、いくつか前提をもうけます。この種の問題を考える際に、とても大切な所です。
- 各回でくじを引く確率は、全て同じである
- 各回で、くじが当たっても外れても、他の回で当たりが出る確率には全く影響しない
- 当たりと外 れが同時に起こる事は無い
このような前提によって、1回ごとの当たる確率を単純に掛け合わせて計算する事が可能となります。実際の所は、1回ごとに当たりの出る確率が全く同じという保証はどこにもありませんし、当たりが出たか外れが出たかで、物理的な影響や心理的な影響が作用する可能性もあります。サイコロであれば、投げ方やサイコロの形、くじ引きであれば混ぜ合わせ方、などが関わってくるでしょう。しかし、こういう理論的な事を考える場合には、一旦その所を措いて、理想的あるいは仮想的な条件が成り立ったとすれば、と設定していくのです。
では、くじ引き100回と書かれたボタンをクリックしてみて下さい。
そうすると、各マス目に、×や○が現れます。もちろん、×が外れ、○が当たりです。文化圏によっては逆の解釈がされる場合もあるでしょうが、日本語話者が直感的に把握しやすいものを選びました。
ボタンを押すと、その下に、 2016年3月20日追記:表の右に配置するようレイアウトを変更しました。ウインドウサイズを狭めたり、スマホなど横方向ドット数が少ないディスプレイでは、縦並びで表示されます 挑戦回数・当たり数・外れ数、のそれぞれが表示されます。ここで注意しなくてはならないのが、当たりの回数が示しているのは、1%の確率で当たるくじを100回引いて1回以上当たった回数である、という事です。え? 解りにくいですか? そうです。この種の問題は、ここが解りにくいのです。
今は、くじを100回引くのを1セットと考えています。ですから、上のくじ引きには、○○セット挑戦と書いている訳です。100回を1回おこなった、と言うといかにも解りにくいですので、100回1セット、と表現し分けています。そして、1回当たろうが100回当たろうが結果は同じと看做します。価値としては、たとえばカードであれば、1枚当たるよりも100枚当たる方が嬉しい場合が多いでしょうけれど、今考えているのは、当たったかどうかで分けていますから、100回全て外れかそうで無いか、の2通りしか考えないという事なのです。
では、ボタンを何回もクリックしてみてください。そうすると、1回以上当たったセット数の、総セット数に対する割合が、円グラフで描画されます。どうでしょう。最初の数回であれば、100%、つまり、円グラフ全体が緑で塗りつぶされるかも知れませんが、回数が増えると、緑色(当たりが入ったセットの割合)とグレー(全部外れたセットの割合)の配分が、大体同じような所に落ち着いてくるのではないでしょうか。
たとえば、100セットチャレンジした所、下の画像のような結果だったとしましょう。
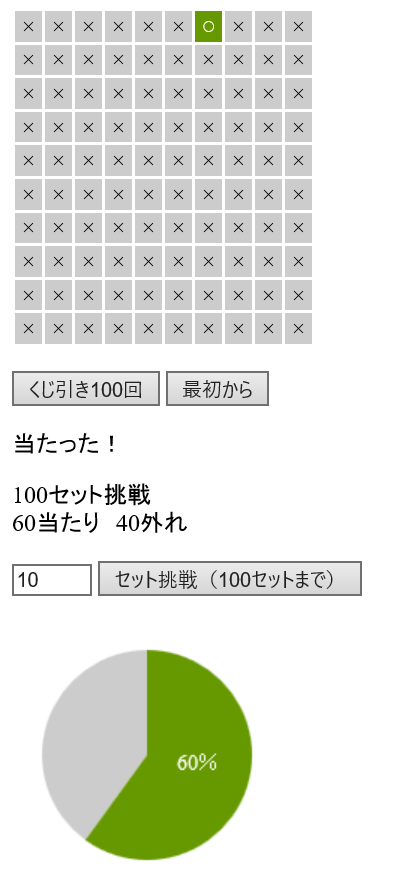
これは、100人が100回のくじ引きにチャレンジした所、1回以上当たった人は6割くらいしかいない、というように解釈出来ます。冒頭で紹介した記事が、まさにこのような事を説明しています。100回くらい引けば1枚くらいは当たるのではないか、といったような直観を確かめるべく実験をおこなった所、それに反するような結果が出た、という具合です。
このような、理論に反するような直観をいだく現象は、心理学ではギャンブラーの錯誤として知られています。たとえばサイコロで、特定の目以外の目が出続けた場合、次には、その出ていない目が出現する確率が高まるのではないか、といったような心理です(参考文献:『心理学初歩(’02)』)。実際、イカサマや、明らかな構造の偏りが無ければ、各目が出る確率は、ほぼ同等(全く同等とは言えない、というのは先述した通り)であるにも拘らず、それが変化してしまうような気がしてしまう、のですね。*1
上で挙げた例だと、たまたま失敗が多かっただけかも知れない、と感ずる方もあるかも知れません。そこで、次の画像も置いておきましょう。
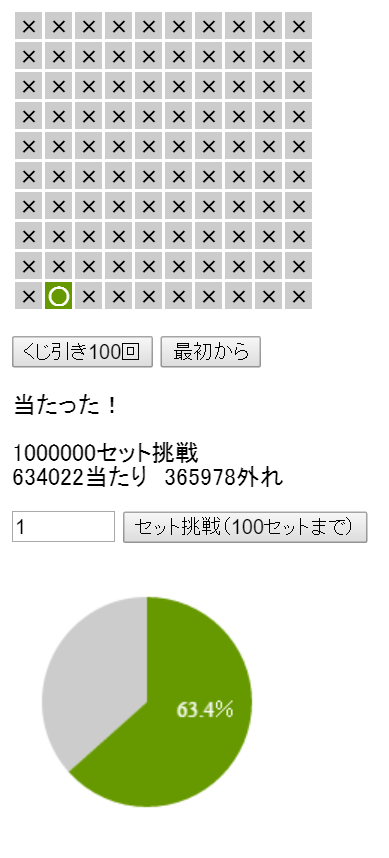
実験的に、100万セット実行してみました。だいぶん、理論的な数値に近いですね。皆さんも、ゲーム感覚で試してみられてはいかがでしょうか。
ところで、今回の例では、くじを、何回当たりが出ようが100回引くというモデルで考えましたが、実際には、色々なケースがあると思います。目当てのカードは何枚あるかとか、同じカードが何枚あってもいいのか、など。目当てのカードが出たらそこで抽選を打ち切る、といった場合も多いでしょう。その辺りの事を考えると、今回の例、冒頭で紹介した記事の例は、最もシンプルな類の問題である、と言えるかも知れません。

確率のはなし―基礎・応用・娯楽 (Best selected business books)
- 作者: 大村平
- 出版社/メーカー: 日科技連出版社
- 発売日: 2002/09/01
- メディア: 単行本
- 購入: 12人 クリック: 158回
- この商品を含むブログ (13件) を見る
今回話題となったゲームも含め、たくさんの分野に、確率の知識は関わってきます。学校で習うような知識が身近のものごとに関わるという好例でもありますので、改めて勉強してみるというのも、大切な事だろうと思います。